Como ahora si que tenemos todo el circuito montado vamos a empezar a probar los sensores.
El sensor de temperatura tiene un problema de tiempo
El sensor de temperatura es un DS18B20 de Dallas, funciona con un bus onewire y no voy a profundizar mucho más, se carga la librería (hay un montón y se lee con el resto de los sensores. Como siempre me concentraré en el punto en el que nos podemos atascar. Desde que pides la lectura hasta que puedes leerla hay que dejar pasar un tiempo. Por defecto el sensor viene configurado a 12 bits y ese tiempo es de 750 milisegundos aprox. Esto es una barbaridad, para leer la temperatura del sensor de ultrasonidos (tres lecturas diferentes en las que hacemos un median) leer y guardar las lectras en la memoria RTC y hacer todo lo que tenemos que hacer en un ciclo de medida estamos empleando unos 200 ms. Recordemos que es un nodo de bajo consumo y que queremos tenerlo activo el mínimo tiempo posible, no podemos esperar con el nodo encendido 750 ms además de lo que ya tardamos en el resto. Tampoco podemos solicitar la lectura en un ciclo y leerla en el siguiente porque estamos desconectando la alimentación. La solución es configurarlo a 9 bits, con lo que el tiempo de lectura baja a unos 97ms, solicitamos la lectura al principio del ciclo, mientras la hace leemos el sensor de ultrasonidos y después obtenemos el valor. A cambio el valor estará redondeado a 0,5 grados en un termómetro que tiene una precisión de +- 5 grados, no parece un gran problema.
El sensor de ultrasonidos tiene un problema de precisión
El sensor de ultrasonidos funciona emitiendo una onda, esperando que rebote en una superficie y escuchando. Midiendo los milisegundos que ha tardado el eco y dicidiendo por dos tendremos los milisegundos que tarda la onda en llegar al objetivo, la otra parte de la ecuación es la velocidad del sonido.
La velocidad del sonido en un gas sigue la siguiente formula:
Siendo gamma el coeficiente de dilatación adiabática, R la constante universal de los gases, T la temperatura en kelvin y M la masa molar del gas. Los valores típicos para la atmósfera estándar a nivel del mar son los siguientes:
gamma = 1,4 para el aire
R = 8,314 J/mol·K = 8,314 kg·m2/mol·K·s2
T = 293,15 K (20 °C)
M = 0,029 kg/mol para el aire
la fuente de esto es Wikipedia, no pretendo hacer un estudio tan profundo, pero se ve claro que es dependiente de la temperatura ambiente y de la «densidad», que tiene que ver con la presión atmosférica.
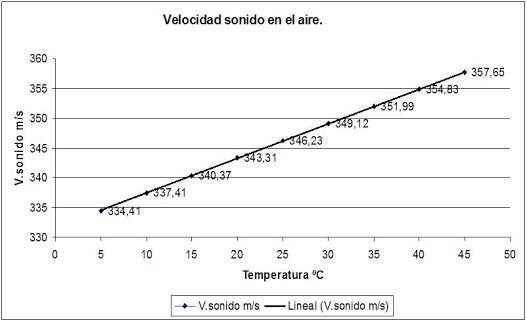
Para no liarnos despreciamos la influencia de la presión atmosférica y consideramos aproximadamente lineal la velocidad de sonido en el aire con respecto a la temperatura, es una buena aproximación.
Velocidad del sonido = 331.3 + 0.606 * temperatura
He puesto esto en un Excel para ver que error estamos corrigiendo por el hecho de compensar la temperatura. El resultagdo es el siguiente:
| Temp | Vel sonido | Distancia sin compensar | Distancia compensada | % error |
| -10 | 325,24 | 0,500 | 0,469 | 6,52% |
| -5 | 328,27 | 0,500 | 0,474 | 5,54% |
| 0 | 331,3 | 0,500 | 0,478 | 4,57% |
| 5 | 334,33 | 0,500 | 0,482 | 3,63% |
| 10 | 337,36 | 0,500 | 0,487 | 2,69% |
| 15 | 340,39 | 0,500 | 0,491 | 1,78% |
| 20 | 343,42 | 0,500 | 0,495 | 0,88% |
| 25 | 346,45 | 0,500 | 0,500 | 0,00% |
| 30 | 349,48 | 0,500 | 0,504 | 0,87% |
| 35 | 352,51 | 0,500 | 0,508 | 1,72% |
| 40 | 355,54 | 0,500 | 0,513 | 2,56% |
| 45 | 358,57 | 0,500 | 0,517 | 3,38% |
Una vez más quiero recordar que no pretendemos crear un dispositivo de medida de precisión, pero esto corrige un efecto estético, en un tanque sin consumo, si baja la temperatura se incrementa el nivel de combustible medido. Supongo que estamos acostumbrados a ver como va bajando el volumen del tanque pero no como sube, lo cual suele llamar la atención.